TP1 - Briques de base (1) - Partie 2

FYI AVERTISSEMENT SUR LE NIVEAU DE DIFFICULTÉ : Le niveau de logique nécessaire pour résoudre les exercices suivants est tout à fait à votre portée. Ces exercices, qualifiés de « Briques de bases », sont donnés à des lycéens en classe de première S et de terminale S.

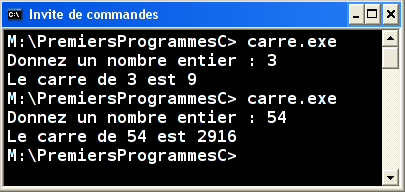
Exercice 1 • Carré d'un nombre

Écrire un programme dans lequel l'utilisateur entre un nombre entier au clavier, et qui affiche le carré de ce nombre

Exercice 2 • Rectangle

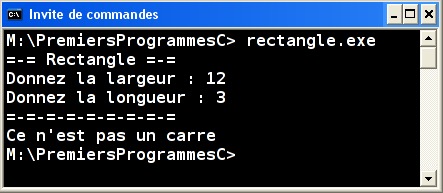
Question 2.1

Écrire un programme qui récupère la largeur et la longueur d'un rectangle au clavier, et qui indique si c'est un carré ou non

Exécution rectangle.exe v1 — Figure 2.1.1

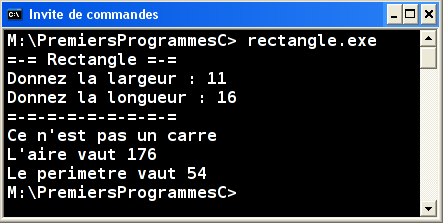
Question 2.2

Compléter ce programme pour calculer l'aire et le périmètre du rectangle

Exécution rectangle.exe v2 — Figure 2.2.1

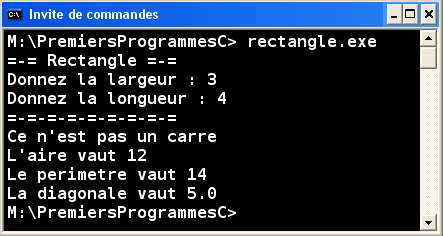
Question 2.3

Compléter ce programme pour calculer la valeur de la diagonale du rectangle

Exécution rectangle.exe v3 — Figure 2.3.1

Exercice 3 • Équations du second degré

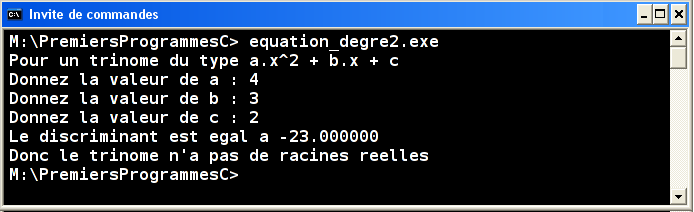
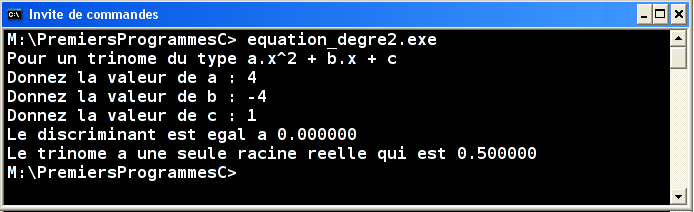
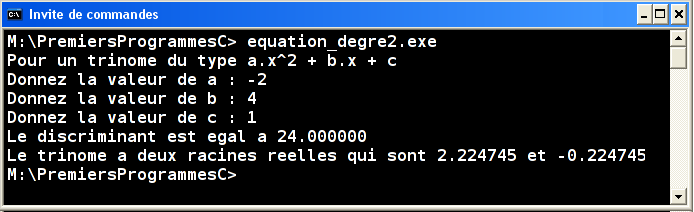
Écrire un programme qui récupère au clavier les trois composantes d'un trinôme a,b,c et qui calcule les racines réelles l'équation du second degré ax²+bx+c

Exécution equation_degre2.exe — Figure 3.1

Exercice 4 • Équations de droite et distance euclidienne

Question 4.1

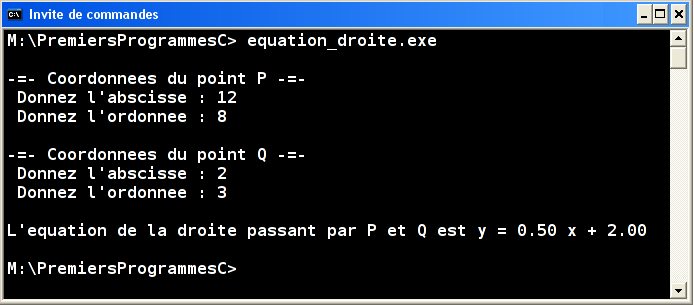
Écrire un programme qui demande les coordonnées de 2 points dans le plan (des nombres entiers, qui seraient par exemple les coordonnées de 2 pixels dans une image) et qui calcule l'équation affine y=ax+b de la droite passant par les 2 points. Le cas où les 2 points ont même abscisse devra être géré séparément.

Surtout, testez votre programme. Par exemple, essayez P(12, 8) et Q(2, 3) et assurez-vous d'obtenir y=0.5x+2

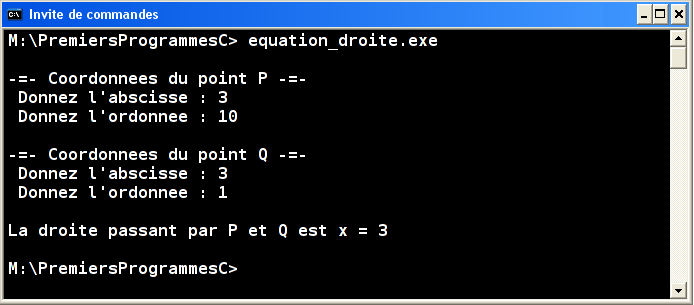
Exécution equation_droite.exe v1 — Figure 4.1.1

Question 4.2

Complétez ce programme pour calculer en plus la distance euclidienne entre ces points.

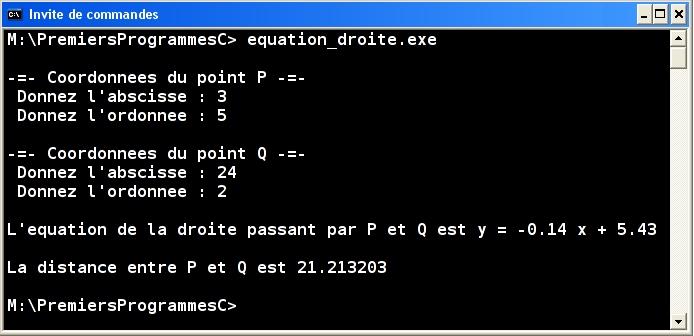
Exécution equation_droite.exe v2 — Figure 4.2.1

Exercice 5 • Années bissextiles

Écrire un programme qui indique si l'année entrée au clavier est, ou n'est pas, bissextile

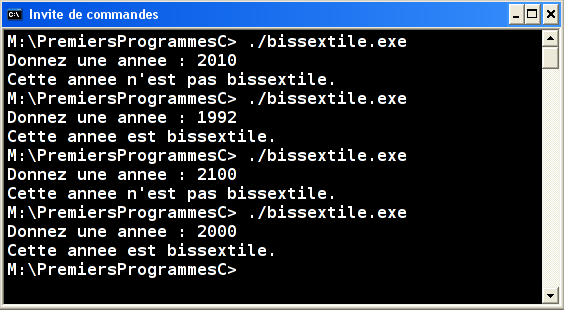
Une année bissextile comporte 366 jours (avec le 29 février). La règle de calcul des années bissextiles, à partir de 1582 et l'instauration du calendrier grégorien, est la suivante :

Règle nominale : Les années divisibles par 4 sont bissextiles, à l'exclusion des années divisibles par 100 qui ne le sont pas. Cependant, les années divisibles par 400 sont bissextiles.

Règle non nominale : Les années non divisibles par 4 ne sont pas bissextiles. Les années non divisibles par 100 sont bissextiles et les années non divisibles par 400 ne sont pas bissextiles.

Par exemple :
• 2010 n'est pas bissextile (car pas divisible par 4)
• 1992, 1996, 2004 et 2008 étaient bissextiles (car divisibles par 4 et pas par 100)
• 1700, 1800 et 1900 n'étaient pas bissextiles (car divisibles par 100)
• 1600 et 2000 étaient bissextiles (car divisibles par 400)